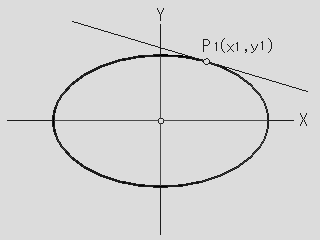
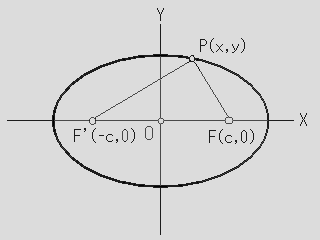 X=0,Y=0を中心とし、傾き=0の楕円を考えてみる。
X=0,Y=0を中心とし、傾き=0の楕円を考えてみる。2つの定点FとF’に至る距離の和が一定になる点Pの取る軌跡が楕円になる。この性質に基づいて、直交座標系における楕円の方程式を導いてみよう。
FとF’を結ぶ直線をX軸に、FF’の垂直二等分線をY軸にとれば、焦点FとF’の座標はそれぞれ、
F(c,0), F’(−c,0)
と置く事が出来る。
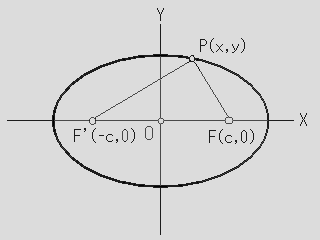 X=0,Y=0を中心とし、傾き=0の楕円を考えてみる。
X=0,Y=0を中心とし、傾き=0の楕円を考えてみる。
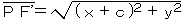
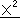 |
+ | 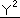 |
=1 |
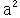 |
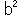 |
 点P
点P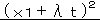 |
+ | 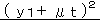 |
=1 | |
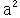 |
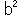 |
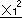 |
+ | 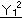 |
=1 | |
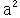 |
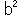 |
 |
+ | 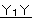 |
=1 |
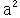 |
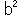 |